



THE POET LONGFELLOW was a fine mathematician who often spoke about the advantage of clothing our mathematical problems in such attractive or congenial garb as would appeal to the fancy of the student in place of following the dry, technical language of the textbooks. He would connect the proposition with some familiar subject which best, explains the problems to be solved.
A clever kindergarten illustration of a mathematical theorem leaves a clearer and more lasting impression upon the mind of a student than a whole term of uncongenial study.
He always held mathematics to be the most important branch of knowledge taught in our colleges and high schools, for the reason that it enters so largely into all of the arts and sciences, and yet the average student graduates with such an undying aversion to figures that, he speedily dismisses all recollections of them from his mind.
The water lily problem is one of several introduced in Longfellow’s “Kavanah,” written while occupying the Chair of Modem Languages in Harvard University, 1849. It is so simple that anyone, without a knowledge of mathematics or geometry, could solve it with a pair of compasses or rule, and yet it illustrates an important geometrical truth in a never-to-be-forgotten way, which many graduates have never grasped at all.
I forget the exact language of the problem, as he described it to me personally during a discussion of the subject, but he told of a water lily growing in a lake, the flower was one span above the surface of the water, and when swayed by the breeze would touch the surface at a distance of two cubits, from which data it was desired to compute the depth of the lake.
Now, let us suppose, as shown in the sketch, that the water lily is ten inches above the surface of the water, and that if it were pulled over to one side it would disappear under the surface at a point distant twenty-one inches from where it now stands, say just where the young lady is supposed to have drawn it, which shows that the two flowers are anchored to the same root at the bottom of the lake, what is the depth of the water?
Euclid says: “That when two chords of an arc intersect within a circle, the products of the parts of one will be equal to the products of the parts of the other.” Therefore in the following illustration the surface of the water forms the chord of one arc, and as the two parts were given as 21 inches, 21x21-441.
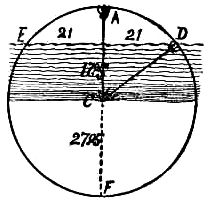
The stem of the lily forms the other intersecting chord, and as its height above the water forms one part of the chord, that part, 10 inches, multiplied by the other part, must be the same as the 441 inches obtained by the parts of the other chord. So divide 441 by 10, and we get 44. 1 inches as the other part of that chord. Adding the 10 and the 44.1, we get 54.1 for the total length of the chord from A to F, which is the diameter of the circle. This we must halve to get the radius, 27.05, but as the flower stood ten inches above the surface of the water, we must deduct that ten inches and we will find that the lake was only 17.05 inches in depth.
2. To Tell a Person's Age.
This method is the easiest and best one known. Let the person whose age is to be discovered do the figuring. Suppose, for example, a girl is 13 and was born in November, put down the number of the month, (November is the eleventh month.)
11
Multiply by 2... 2
----
22
Add 5........... 5
----
27
Multiply by 50.. 50
----
1350
Add Age (13).... 13
----
1363
Subtract 365.... 365
----
998
Add 115......... 115
----
1113
As she answers 1113, tell her her age is 13 and November is her birth month. This test never fails up to 100. In computing ages under 10, a cipher will appear prefixed in the result, but no notice is taken of it.
3.
Why would an owl be offended at your calling him a pheasant? Because you would be making game of him.
[Page 93]