



JUST TO SHOW HOW the average mortal follows the cut and dried rules for doing ordinary calculations and will be puzzled by simple problems which call for original lines of thought, attention is called to this practical example which requires only a slight knowledge of the most elementary arithmetic. By a kindergarten process it can be explained in a few minutes so that any child can do it, and yet I hazard the opinion that ninety-nine out of every one hundred of our shrewdest business men would fail to figure it out in a week. So much for learning mathematics by rule instead of common sense which teaches the reason why!
I went to a ferry a short time ago to investigate the relative speeds of two boats, and by calculation evolved the following information: The two ferry boats started from opposite sides of the river at the same instant. One boat, however, was faster than the other, so they met at a point just 720 yards from the shore. Each boat remained but ten minutes in the slip to change passengers and then started on its return trip, when, by careful calculation, I found that they now met at a point just 400 yards from the other shore.
From the data given, our puzzlists are asked to show a simple way of determining the exact width of the river.
Regarding that ferryboat puzzle, I promised to show how the problem can be solved by common sense and simple addition, which I will proceed to do by reference to the following diagram:
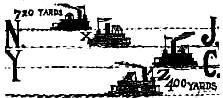
It was told that the two ferryboats started simultaneously from the sides of the river and met at the point X, just 710 yards from the New York shore. A glance at the sketch clearly shows that the combined distance which both have traveled is equal to the width of the river and that the black boat has gone 720 yards. Well, they continue their journey and reach the opposite shores, and the distance traveled is equal to twice the width of the river. The amount of time consumed at the landing is of no consequence and does not affect the problem. They started on their return trip and meet at Z, as shown. Now, the distance traveled by both is equal to three times the width of the river, as shown by the lines, so it is obvious that each boat has gone three times as far as when they first met, and had made but one width. The black boat had then gone 720 yards, so it has now gone three times that distance, viz., 2,160 yards, to Z. This the sketch shows to be 400 yards more than the width of the river, so all the mathematical work we are obliged to do is to deduct 400 from 2,160 to find that the river from New York to Jersey City is 1,760 yards wide, which is exactly one mile. Without the aid of algebra, geometry or mathematics, we have solved by elementary kindergarten arithmetic a problem which would baffle half the mathematicians in the city.
2. A Parlor Trick.
Robert Heller had the happiest faculty of showing a card trick to its best advantage of any performer I ever met.
Writing the name of a card on a piece of paper, he would fold, without showing or naming, and handing it to one of the spectators, tell him to stow it safely in his vest pocket.
Let us suppose he has determined to make you choose the deuce of diamonds, which he has written upon the paper. Holding the pack in his hand, he says: ÔÇťHere are fifty-two cards ÔÇ” twenty-six red and twenty-six black. Which color do you prefer?ÔÇŁ if you say black, he throws down the black, and says, ÔÇťThat leaves me the red.ÔÇŁ But if you had said red. He would throw down the black cards all the same, and would say, ÔÇťAll right, here are the red.ÔÇŁ Then he would say. ÔÇťThere are thirteen hearts and thirteen diamonds. Which do you want?ÔÇŁ If you say ÔÇťhearts,ÔÇŁ he throws them down as before, and says, ÔÇťI will keep the diamonds,ÔÇŁ and he would have worked the game as previously described if you had preferred diamonds.
Then he would say, ÔÇťHere are six cards, and here are seven, Which shall we keep?ÔÇŁ
Of course he keeps the six low cards, and dividing again, asks, ÔÇťDo you select, the low cards or the high ones?ÔÇŁ
Discarding as before, he places the ace, deuce and tray together and asks, ÔÇťWhich card do you select?ÔÇŁ
The second is chosen, and he says, ÔÇťLook at the paper!ÔÇŁ But if the others had been chosen, he would say. With equal effrontery, ÔÇťAll right, that leaves me the deuce. Look at the paper!ÔÇŁ
[Page 80]