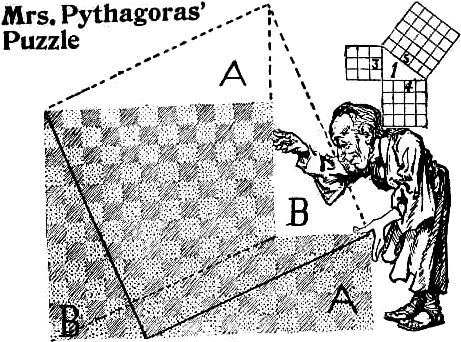
When Mrs. Pythagoras took counsel with her spouse regarding the way of squaring a two-square formed remnant of Athenian matting, the great philosopher explained: “Knowing that a square erected on the hypotenuse line of a right-angled triangle is equal to the square of the base and the square of the side combined, we see that the square you require must be equal to both squares, and therefore must be equal to the square of the hypotenuse.”

The truth of this great theorem is shown in the small illustration. No. 1 shows a right-angled triangle; being three inches high, the square of that side contains nine square inches; the base, being four inches long, contains sixteen square inches, and the five inch hypotenuse square contains as many square inches as both of the other squares added together.

If we wish to make one square out of two we merely place them together and draw a straight line from the top of the smallest and draw the line through the larger to the lower comer, B to B, and it will form the hypotenuse line of a triangle, giving the length of the square which will be equal to both of the other squares. A beautiful demonstration is shown in three pieces by clipping off the triangular pieces and fitting them above as shown. It will always make a perfect square from any two-square shaped piece of paper.

When this principle is thoroughly understood any number of squares or circles may be added together at a glance.

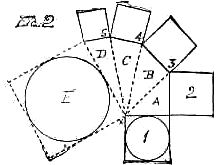
In the above illustration 1 and 2 would form a square equal to the hypotenuse line of A. Squares 3, 4 and 5 are each added to the hypotenuse lines, showing that the square E is as large as the five small ones. All manner of forms, like rhomboids, pyramids, crosses, etc., can be transformed into squares by this method, which is invaluable in the world of puzzledom. In the following small figure of a cross we see that the lower square X would fill the upper space X, thereby forming a two-square form, which we know how to transform into a square which we can see must be of the dimensions of that dotted hypotenuse line.

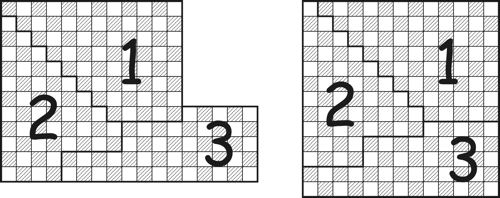
But to get back to Mrs. Pythagoras' matting puzzle, which the great philosopher offered to solve upon the principle of Euclid’s 47 proposition known as pons asinorum. “Now, Thag,” says she. For she always called him that in the house, “I am feared these goods will fray if they are cut on the bias, so I want to get along without that hippopotamus line. Here is a plan which will also do it in three pieces:

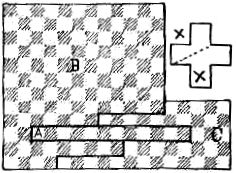
“Cut out that long piece marked A, and stand it on end at one side; then move the piece down one step, and it forms a 13x13 square, all right, all right.

“But, I don't like it altogether, Thag; you see the pattern don't run quite right on the squares in that long piece. Can't you find a perfect answer without giving any of the squares that half turn? I know it can be done.”

There we have Mrs. Pythagoras’ new puzzle.

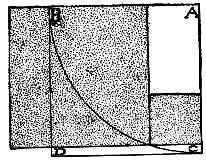
On the principle that every good rule should work both ways, we will now reverse the idea so as to produce two squares from one large square. Place the point of the compasses at A and describe the arc B C and any point on the arc will indicate the junction of the two smaller squares, which are equal to the area of the largest A B D C, and brings us back to a two-square form of any desired dimension.

It is easy to prove the truth of Euclid’s famous proposition by erecting four triangles around the hypotenuse square C. The area of the large square being (A + B)² equals A² + 2AB + B²; subtracting the contents of the 4 triangles 2AB proves A² + B² of the side and base equals C² of the hypotenuse.