


Eminent archaeologists and antiquarians like Le Plongeon, Schliemann, Prof. Wilson and others show that prehistoric man must have hit upon the crude sign of two crossed marks to indicate a human emblem, just as we in many instances employ peculiar brands or marks for similar purposes.
My present object, however, is to give a discourse upon those ancient emblems which have evolved the geometrical proportions of the Greek or mundane cross, which for upward of six thousand years has stood for the symbol of human intelligence, and is now recognized as representing science and mathematical exactitude. The symmetrical cross formed from five squares for thousands of years has been known as the Hindoo problem. By cutting it in five pieces, upon the principle of Euclid's forty-seventh proposition, it will form a square. Almost all puzzle books give the scientific clipping of the four corners as shown by Fig. A to form the square B.
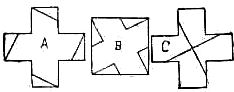
When a puzzle, however, can be done “a shorter way,” “in fewer pieces,” or “in less moves,” it is said to be “cooked,” or, in puzzle language, “busted.” Well, when I told the head of Harvard College that the symbol which was incorporated in the Harvard seal could be converted into a square by making four pieces instead of five, I was informed that the feat was impossible.
I used it as an advertising puzzle, offering a hundred dollars for the shortest method of converting the Creek cross into a square. Several hundred thousand answers were received employing five pieces, but not one answer that showed how to do it in four. Fig. C shows how the four pieces should be made.
I afterward discovered that there was an infinite number of answers, as the parallel cut may be made anywhere on the lines shown, and the perpendicular cut at any right-angled point of intersection.
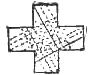
The four segments will always fit to form a perfect square, so the puzzle makers can exercise their ingenuity by introducing conditions or stipulations which will bare out all other answers but the one intended. In the illustrations given it is asked to divide a cross in four equal parts which will form a square. In a second puzzle it was said “to divide a cross, with two clips of the scissors, in four pieces, which will form a square.”
There are numerous other problems connected with the symmetrical proportions of the Greek cross which make a most valuable lesson in the theory of all cutting puzzles.
A beautiful requirement is to divide a square in five pieces which will form two crosses. Fig. 1 shows how to produce five pieces which will form two crosses. The center piece makes a new cross, and the four outside pieces wall form another. But, after the puzzle had become famous, I found a second way in one piece less, as shown in Fig. 2.
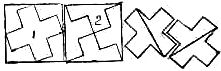
Another wav to vary the stipulations so as to form a beautiful puzzle calls for the dividing of a square in five pieces which will form two crosses of different sizes.
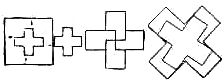
First cut out the little cross, then divide the remainder in four parts which will form the large cross, as shown. The fourth figure shows the puzzle of cutting a cross in five pieces which will form two crosses of equal size, and is one of the most beautiful problems of the series.
It is a most remarkable fact that a mysterious affinity or relationship can be shown to exist between all the ancient signs and symbols, in that each one can be converted into another by some subtle change which constitutes a clever puzzle. The Swastika can be changed into a square, the square into a cross, the cross into a triangle, an oblong or several crosses, and from these we can form a star, a crescent, oval, a monad, and from that a circle, which looks very much as if the squaring of the circle was one of the mysteries pertaining to the mystic signs and symbols.
2. A Puzzle.
My tongue is long, my breath is strong,
And yet I breed no strife.
My voice yon hear both far and near. And yet I have no life.
Cipher Answer.— 2. 5, 12, 12.
BELL
3.

In describing his experiences at a bargain sale, Smith says that half of his money was gone in just thirty minutes, so that he had pennies where he had dollars before, and but half as many dollars as before he had pennies. Now, how much did he spend?
Smith must have started out with $99. 98, and spent all but $49. 99. Now he has many pennies as he before had dollars and half as many dollars as he previously had pennies.
[Page 58]