EVERYONE is familiar with the time-honored puzzle of the ship's carpenter who had to place a square hole by cutting a 9x16 bit of wood into two pieces. It forms a valuable and interesting lesson in puzzle-making which is well worth knowing as it will enable you to originate or readily solve other puzzles of that class.

Oblongs of any desired proportions may be formed by measuring off the side of a square into a given number of spaces; then marking off the base so as to contain one space less, so they will be greater in width than height. Then mark the square and cut down on the steps as shown,

and the two pieces form patterns for new puzzles to be divided into two pieces to be made into squares. Here is the carpenter and below him the two boards that make two squares.

In solving puzzles of this kind the dimensions of the required square and can be obtained by multiplying the side by the base, which, as in the case of the carpenters puzzle: 9x16. and 4x9, or 8x12.5 will always produce a square number. By the puzzle process of working backward, we see that the base of the oblong must be divided off into a certain number of spaces, slightly larger, and containing one more space than the side to make the steps form a perfect square.

It is easy to guess the number of spaces for the side and base, but to reduce the problem to an exact science, it is well to apply the following rule for squaring rectangles:

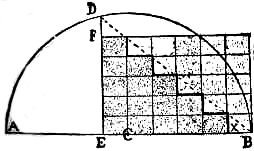
To the length of any rectangle add the width, so as to obtain the distance A to B, then with a pair of compasses placed at the center C, describe the semicircle B A. The intersection of the arc with the line from E to D gives the correct size of the square to be built from the rectangle. The distance from D to F shows the size of the spaces to be represented on the side of the rectangle, so we find in this case it will measure five of such spaces, and as the base must contain one more space, we divide it off into six. The difference in length between E to B and E to D would represent the width of the required spaces on the base line. The above formula solves any rectangle that was built from a square by the carpentering process, but the Euclidian rule which performs the feat in three pieces from any rectangle is to cut on the dotted lines—on the bias—-from B to D; slide up the top piece and clip off the little corner X to patch with. It is a beautiful rule with which all puzzlists should be familiar, so now that you understand the principle, can you square the two illustrations given?

2.

A kind lady who dispensed charity every week to some needy persons hinted to her pensioners that each would receive two shillings more if there were five applicants less. Each mendicant endeavored to persuade the others to keep away. Nevertheless, at the next meeting every one was on hand, and four new applicants, so that every one got one shilling less.

Can you tell how much each one received?