



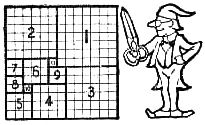
SOMEWHAT IN THE nature of a rest from study, we will call attention to the Patch Quilt puzzle as bring a companion piece to Mrs. Deacon White's remnant problem. The sketch represents the members of the “Willing Workers” society overwhelming their good parson with a token of love and esteem, in the shape of a beautiful patch work quilt. Every member contributed one square piece of patchwork consisting of one or more of the small squares, each of these contributions being perfectly square in shape, involved a pretty puzzle which nearly disrupted the society.
Any lady would have resigned if her particular piece of work was tampered with or omitted, so it became a matter of considerable study to find out how to unite all of the squares, of various sizes, together, so as to form the one large square quilt. Incidentally it may be mentioned that as every member contributed one square piece of patch quilt, you will know just how many members there were when you discover into how few square pieces the quilt can be divided. It is a simple puzzle which will give considerable scope for ingenuity and patience.
The following diagram shows how the 13x13 quilt can be divided into eleven smaller squares, which is the least number of square pieces which it will divide into without destroying the checkered pattern. It proved to be a difficult puzzle, and those who discovered the correct answer, found that there was a certain mathematical principle involved, which held them close to the rules of square root.
2. The Lost Cent.
Here is a puzzle known as the Covent Garden Problem, which appeared in London half a century ago, accompanied by the somewhat surprising assertion that it had mystified the best mathematicians of England. The problem is continually cropping up, in some form or other, generally accompanied by that same statement of its having baffled the European mathematicians, all of which must be taken with a liberal allowance of salt, as our Yankee scholars would find such little difficulty in dispelling the mystery that I can only feel justified in presenting it as a special practice problem for our more juvenile puzzlists. As some of the other puzzles have proven to be too difficult for many beginners who have become interested in such matters. I have determined to act upon an oft-repeated suggestion from our younger friends to present a few simple problems of a mathematical nature winch all should be able to solve.
Well, to get back to the Covent Garden Problem, which I had almost forgotten. It is told that two huckster ladies were selling apples at the market, when Mrs. Smith, for some reason or other which must be the real mystery which has baffled the mathematicians, was called away and asked Mrs. Junes, the other apple lady, to dispose of her stock for her
Now, it appears that they each had an equal number of apples, but Mrs. Jones had larger fruit and was selling hers at the rate of two for a penny, while Mrs. Smith sold three of hers for a penny. Upon accepting the responsibility of disposing her friend's stock. Mrs. Jones, wishing to be very impartial, mixed them all together and sold them off at the rate of five apples for two pence.
When Mrs. Smith returned the next day the apples had all been disposed of, but when they came to divide the proceeds they found that they were just seven pence short, and it is this shortage in the apple or financial market which has disturbed the mathematical equilibrium for such a long period.
Supposing that they divided the money equally, each taking one-half, the problem is to tell just how much money Mrs. Jones lost by the unfortunate partnership.

To tackle the problem from a somewhat new standpoint it can readily be shown that the apples, if sold at 1/3 of a penny and 1/2 of a penny, would average 5/6 for two, or 25/60 of a penny for each apple, but as they were closed out at the rate of five apples for two pence, which is the same as 2/5 or 24/60 of a penny per apple, then 1/60 of a penny was lost on every apple. As it was stated that seven pence was Iost, we will multiply that 60 by 7, which shows there must have been 420 apples, of which they each had one-half. As Mrs. Jones had 210, for which she would have received 105 pence, but only got one-half of the proceeds of the entire sale at the rate of 5 for 2 pence, viz.: 84 pence, she lost twenty-one pence, while Mrs. Smith, who should have received but seventy pence for her three-for-a-penny fruit, actually gets eighty-five.
The mysterious discrepancy occurs at the end of the seventieth combination sale. Mrs. Smith’s cheap fruit becomes exhausted on the seventieth sale, which takes 210 of three-fors, and 140 of the two-fors, and at that stage of the game Mrs. Smith was entitled to half of the proceeds, and should have withdrawn with her seventy pence. As there were now just seventy of the better class stock left, every sale now involves the giving of three apples for a penny, which should sell for two for a penny, Mrs. Jones’ stock is sacrificed.
[Page 39]