



REPLYING TO THE oft-repeated query as to how puzzles are originated; whether they come spontaneously like sudden inspirations or as the result of long and careful study, I would say that like the development of any other inventions, they come either way; from a happy thought or from hard work, although in either case the idea is generally suggested by some chance incident.
By way of illustration I will say that during my summer's outing, while scouring the country en-wheel, I ran up against a good-natured Hibernian whose apple orchard and spring of cool water made his little shanty a veritable Mecca for weary bicycle pilgrims. He was a unique character, and few of us ever came out first best with him in a passage of wits, as he had an inexhaustible stock of replies at his tongue's end ready for anything that could be fired at him.
It will be interesting to know how he takes to the idea of being immortalized in print when he sees the sketch I made of him seated in characteristic pose at the door of his domicile. The original picture, neatly framed, has been sent by express to pace his “drawing room” in acknowledgment of “one on the puzzler.”
You see, I was so foolhardy as to intimate that there was a certain bond of fellowship between us because we both made our living by the pen. Which seemed to touch him in his most tender spot, for he asked in his earnest way if I knew why an Irishman always builds a pig pen under the drawing room window? Then, after I had suggested every practical explanation and completely exhausted my repertoire of conundrums, appropriate or otherwise, he told me in a confidential whisper which could be heard a mile that “it was built there to keep the pigs in.” He begged me not to tell the reason to the rest of the party, who might think it a joke. During the journey home there was not one of that party who did not fall off his bicycle a dozen times in thinking over Pat's problem. Of course I thought of it as well, and there was one statement concerning his pigsty which struck me as being so “odd” that I utilized it to get even on the rest of the crowd. I can not tell it in Pat's own language, but it appears that, believing with Rory O'More in “the luck of odd numbers,” he had made it a rule to “bring up.” as he suggestively termed it, just twenty-one pigs every season. To accommodate them he built the pen under the drawing room window, dividing his happy family into four groups, so that each pen contained an even number of pairs and one odd pig. It looks like an easy little problem to divide twenty-one pigs in that way if you say it quirk, but just try it!
If you understand the mystery of Shakespeare's “divinity of odd numbers,” show how Pat placed his twenty-one pigs in four pens so that each pen contained that odd little porker.
Pat's pig sty puzzled many clever mathematicians as well as puzzlists who failed to place twenty-one pigs in four pens so that there will be an odd number of pigs within each pen. As well as an even number of pairs. Clever puzzlist hit upon the necessary expedient of “nesting” the pens one inside of another, but the feature of saying that each pen must contain “an equal number of pairs,” as well as the fact of the outside pen, which is in sight, holding not less than five pigs which can be seen, spoiled some of the answers suggested.
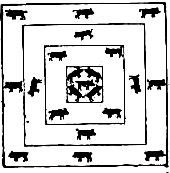
The only possible answer is to place five pigs in the center pen, viz.: two pairs and an odd pig. Then build a pen round that pen and place four pigs in it, a third pen surrounds that one, also with four pigs, and the fifth pen with eight pigs encloses the other pens, and as a matter of fact contains the entire twenty-one pigs!
2. Peterchen's Pretzel

Here is a simple little marking problem for the juveniles who have found the other problems somewhat difficult. Little Peterchen had a Vienna twisted pretzel, as shown in the drawing, and asks his young friends to guess into how many pieces he divided it with one straight cut with a knife. Supposing it to be a real pretzel, draw a straight line which would divide it into the greatest possible number of pieces.

The pretzel can be divided into ten pieces as shown:
[Page 37]