



SPEAKING ABOUT the way that puzzle ideas come to us it may be said that the theme for a good puzzle can be suggested by anything striding or novel that one chances to see, but the application or proper working out of the scheme may require considerable time and study. Something in the ordinary affairs of life puzzles us a little by its oddity, and the thought naturally occurs, “If this thing perplexed me in its accidental form, when no feature of difficulty was intended, how would it be possible to increase the difficulty by dressing it up in true puzzle form so as to conceal the principle involved?”
The problem must be posed in pleasant shape, so that the picture aids in explaining the terms and at the same time conceals its real difficulty by imparting what Bret Harte would term a “childlike and bland” simplicity to the whole story. The very name may be utilized to draw attention away from the trick, for, as an old philosopher remarked several centuries before they spoke United States, “Ars est celare artem,” by which he meant to inform puzzle-makers that the true art is to conceal the art. Therein lies the main difference between modern and old time puzzles.
Chancing one day to be in a commissary department when an assistant was portioning out cheese, I was struck by the ingenious way which he divided it, and the more I thought it over the more firmly I became convinced that I was indebted to the visit for a happy suggestion which would eventually crystalize into puzzle form. I complimented the quartermaster upon the skill of his assistant, to which he replied: “Oh, that is nothing! You should see him cut pie!”
I never had the opportunity of witnessing his proficiency in the dispensation of pie, but it seemed as if a piece of pie and cheese had got stuck in my crop and disturbed my mental digestion from that moment, until one day being called upon to produce an original puzzle, I drew a circle and called it the legend of the boarding house pie, which has since become famous.
The cutting of a piece of pie pertains only to the superficial surface, as it goes no further than square root or the second power, as the mathematicians would say. In the portioning of cheese we go below the surface into cubic equations known as the third power, for we have to consider the feature of depth.
Can you tell how many pieces are produced by the following six straight cuts?
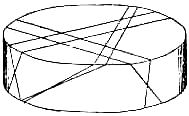
The cheese is divided in two pieces by one cut, into 4 by the second; 8 by the third; 15 by the fourth; 26 by the fifth, and 42 by the sixth.
2. Passing the Japanese Mines.
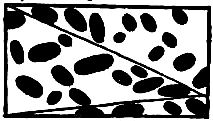
The section of a chart of Japanese mines placed at the entrance to the harbor of Port Arthur is presented for the benefit of the young puzzlists, who are asked to show how a vessel might pass from the bottom to the top of the picture by changing her course but once. Draw a straight line from the bottom of the picture to a certain point, from which you can draw another staight line to the top, so that the two lines will indicate a safe channel through the twenty-eight, mines or torpedoes.

The Japanese Mines may be crossed by two straight lines as shown:
[Page 34]