I STARTED two watches at the same time and found that one went two minutes an hour too slow, and the other one minute an hour too fast, so that when I looked at them again the faster one was exactly one hour ahead. Can you figure out from the dial at what time before noon the watches must have started?

Here is another one which will puzzle you: How soon will the hour, minute and second hands again appear the same distances apart, as shown above?

Such problem are built upon the immutable laws of the divisions of time and are therefore purely mathematical and mechanical. There are 60 seconds to a minute, and 60 minutes to an hour, therefore there are 3,600 seconds to an hour, and that is all there is to it, although there are many clever and very puzzling problems connected with watches and clocks. When I was a very little lad I learned that a pendulum 39.1 inches long would beat a true second. I was very fond of running so I used to carry a bullet attached to a string of that length, which would swing from a pin stuck in the fence so that I could time the boys racing. I became infatuated with the sport and have run many races in all quarters of the globe and in innumerable cases can thank the early training of my legs for saving my skin, and at times my life.

I may say, while upon the subject, that to run 100 yards in 9 seconds is the limit of speed. I have seen it run in that time, but there is no professional living who can do it. Amateurs and smart boys, with the aid of a bullet and string will find their speed to be somewhere between ten and twenty seconds, and may derive great pleasure, as by constant practice they reduce their record down the fraction of a second at a time.

For practical use the bullet and string may be 9.8 inches long then it will count half a second in its swing from right to left, or one whole second in the swing of forward and back; this enables one to count the half and quarter seconds.

The remarkable fact of a 39.1 pendulum beating a true second in its swing, whether it travels two feet each time, or one foot, or only, one inch, is the principle which regulates all clocks, and even watches. The hair spring connected with the escapement of a watch utilizes the elasticity of the spring in place of gravity.

The only obstacle to perfect time indicating is that the pendulums lengthen when the temperature is warm. This fault is overcome by ingenious compensating devices for correcting the length of the pendulum by the use of two metals of different expansive power.

I once constructed a clock out of wood which kept excellent time. Here is how I utilized the “gridiron” principle to regulate the center of oscillation. The rods A A are made of wood which expands but little from heat, B is made of metal which expands twice as much, so where A lengthens the pendulum a little, B expands twice as much and shortens it again.

Pendulums must be of different lengths in different parts of the earth on account of the variable attraction of gravitation. The rule for getting the length of a pendulum is known by mathematicians as “pi times the square root of the length of the pendulum (in inches) divided by gravity.”

A falling body goes 16 feet the first second; 3 times 16 the next second . 5 times 16 the third second, and so on increasing according to the odd numerals, 7, 9, 11 times as fast, and by this rule we make our clocks and watches! Here is a pretty problem to conclude with for the expert mathematicians to ponder over: If a pendulum vibrates as often in a minute as it has inches in its length, how long is it?

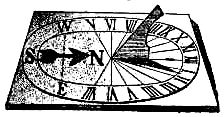
The watch was invented at Nurnberg at the end of the 15th century, but was of no practical value until Dr. Hooke invented the hair-spring in 1658. The time-keeping qualities of a watch depends altogether on the perfection of the escapement which performs the pan of a pendulum. I have a $1,000 Jorgenson repeater which rings the hours, quarters and minutes; times the horses and does all sorts of stunts. The manufacturer of an American watch presented me with a time-piece and asked me to keep a careful tally on the two watches for three months; I did so, and cheerfully give credit to the American product which beat the other out by one minute and ten seconds. To show my sporting blood, I offer to put up that watch against the best chronometer in the world, the one which keeps the best time for three months to take both watches. As boy I remember rending about the days when they depended upon hour glasses and sun-dials, so I constructed a sun-dial which kept perfect time. Here is a pattern for the clever lads to follow after, which calls for no particular directions: Just paint the dial, as shown, upon a piece of board; let the pointer run up about at an angle of 45 degrees; set the dial very level with 12 pointing exactly north and the shadow indicates the hour. In the sketch it is pointing to half past one.