



OF COURSE, ANY ONE who has ever presented a puzzle or trick to a party of friends is acquainted with Alec and his habit of showing, or attempting to show, that he knows all about the trick before it has been explained. In case he happens to have seen the puzzle, he gives away the answer before those who take interest in such matters have a chance to try it. Even when it is new to him, he aims to show how it resembles something else which he can readily demonstrate to be superior to this one. Generally his explanation reminds us of the Persian proverb of “He who knows not, and knows not that he knows not, is a nuisance,” and it is a pleasure to squelch him, as in the following instance:
Harry is about to show his young friends a clever cutting puzzle. When he is rudely interrupted by Alec the Terrible, who believes it to be what is familiarly known among puzzlists as the famous old Mitre puzzle, which I sprang upon the public over fifty years ago, wherein the paper is to be divided into four pieces of similar shape and size.
In response to Alex's boisterous offer to explain the puzzle to every one, Harry promptly replies:
“All right! The puzzle is to cut this paper into the fewest possible number of pieces which will fit together so as to form a perfect square. I have forgotten the answer myself, but my friend here has kindly volunteered to explain it, so as to enable you all to win the handsome prizes which have been offered.”
The puzzle is not so easy as it looks, and is liable to baffle an expert a long time before he hits upon the correct answer. The student will speedily discover that the principle of our old friend Pythagoras' problem is the key to the situation, in that it gives the size of the square to be formed.
Of course, there are innumerable ways of doing the feat by cutting the paper into many pieces, so you will readily discover one of these answers. Herein, however, lies the merit of the modern school of puzzles which gives great scope for ingenuity and skill, for while any one may find a fairlv good answer a more clever puzzlist has an oppurtunitv to discover a better one.
The Smart Alec puzzle, as was intimated, proved to be a difficult task to master by purely experimental methods, although, as was explained, a knowledge of Pythagoras problem Is of use in discovering the answer.
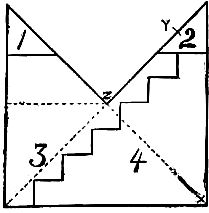
Pythagoras' rule will give us at least the size of the square to be formed, for if we divide the paper into four pieces by cutting in the dotted lines, we know that 2 and 4 will make one square, while 1 and 3 will form a smaller one. Placing the two squares together, according to the manner explained some time ago, the hypothenuse line from the corner X to the top of the smaller square at Y gives the size of the new square.
To solve the puzzle, however, in the fewest possible number of pieces, first clip off the little pieces 1 and 2 and pack them into the center. Then cut the zig-zag steps, and move the piece No. 4 down one step and the four pieces fit together so as to make a perfect souare. There are numerous ways of performing the feat with from five to a dozen pieces, but the answer as given is both difficult and scientific.
2. Quarrelsome Neighbors
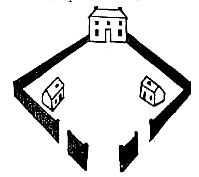
Here is an odd little puzzle for the Juveniles, which is interesting as being one of my earliest productions, published more than half a century ago. It shows the original drawing as done by a Lad of nine and is given to encourage young puzzlists to attempt similar work. It is told that three neighbors, who shared a small park, as shown in the sketch, had a falling out. The owner of the large house complaining that his neighbor's chickens annoyed him, built an enclosed pathway from his door to the gate at the bottom of the picture. Then the man on the right built a path to the gate on the left, and the man on the left built a path to the gate on the right, so that none of the paths cross!
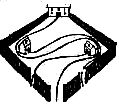
The Quarrelsome Neighbors made their paths as shown in the accompanvine sketch;
[Page 27]