



AS SHOWING HOW our earliest impressions cling to us through life. I recall that in addition to the pardonable pride which all Americans felt n the name of General Winfield Scott, my infantile imagination was fired by my father's holding me up on his shoulders during a military procession to see the hero who whipped the British at Chippewa and Lundy's Lane. I do not think that my mind has ever been entirely disabused of the impression then created, that General Scott was the greatest man that ever lived. The idea was probably intensified a year later when, during our war with Mexico, in 1847, father gave me a dog, and, as a matter of course, no boy ever forgets his first dog. It was given to me on the day of the battle of Monterey, and was appropriately christened “Monterey Scott.”
When the Civil War came on in 1861, I, in common with others. Predicted that General Scott would quell the war in short order. But our hero, who was born in 1788. was too old and infirm to stand the brunt of active service, and was compelled to transfer the leadership to McClellan.
Many yet live, however, who remember the sensation created by General Scott's remarkable saying to Secretary of War Stanton, to the effect that; “While we have scores of commanders who could march a division of soldiers into a park, not one of them knew enough about military tactics to get them out again!”
The remark was accepted as a scathing criticism of what were termed our holiday parade soldiers.
I knew the veteran hero as a skillful chess player, and now recall the fact of building a curious chess puzzle, which I intended to present to him, if occasion occurred, to illustrate the military tactics of a division of soldiers passing through a public park.
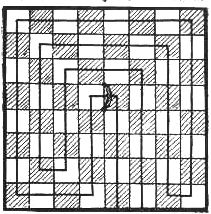
It does not require a knowledge of the game, as it is a puzzle, pure and simple; but to facilitate explanation, I have taken the liberty of marking the park off into squares, which resemble a checker board. The problem, however, is quite pretty: Show how a military division should enter at gate No. 1, march through all of the squares under the triumphal arch, and out through gate No. 2, making the fewest possible number of turns.
Mark an 8 x 8 diagram of 64 squares upon a piece of paper and then essay with a pencil to pass over every square beginning and ending at the gales shown, and it is safe to say you will make several attempts before you get the shortest possible answer, which is so pretty that you will know when you have guessed it.
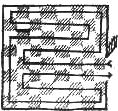
As a further elucidation of this same scheme which is suggestive of many other equally good ideas, let us look at the following puzzle which we will term “The Wanderings of Paddy's Pig.” You see the garden gate was left, open so that his pig-ship entered and rooted up sixty-four bills of potatoes and escaped by the same gate, after making what might be called 21 right-angled moves without crossing that black bar.
I am sure that the trick can be done in less than twenty-one moves and it is given as a puzzle for you to find out the fewest possible number of turns that the pig had to make to get all of the “murphies.”

That lesson in military tactics, wherein a military division was to enter the park at one gate, go through the sixty four-squares and out at the other gate after passing under the triumphal arch in the center of the field, was sufficiently difficult to amuse and interest our young puzzlists, who found that there was but one way to perform the feat in fifteen moves, as shown, although there are a thousand and one routes which call for just on extra turn.
Paddy's pig made 14 turns, as shown:
[Page 21]