



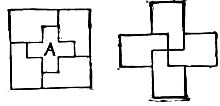
HERE IS A PRETTY little cutting puzzle, which is said to have originated in the mind of a Red Cross lassie while serving in Uncle Sam’s Ambulance Corps. It is safe to say that, the bright witted little volunteer must have been a lineal descendant of Betsy Ross, who, it will be remembered designed the five-pointed star with one deft clip of her scissors. In the present instance it was necessary to practice strict economy in the manufacture of the red crosses to decorate the arms of the nurses, for the reason that the supply of red flannel was running very short in camp, so the problem presented is as follows: Take a square piece of paper and without any waste cut it into five pieces which will fit together so as to make two Greek crosses of same size.
The Red Cross puzzle showed how to make two crosses of the same size, so we will now make two crosses of different sizes:
2. Progressive Conundrums.
‚ÄúMiss Gracie,‚ÄĚ he said, with an engaging smile, ‚Äúdid you ever try your hand at one of these progressive conundrums?‚ÄĚ
‚ÄúWhat is a progressive conundrum, Mr. Spoonamore?‚ÄĚ inquired the young lady.
‚Äė‚ÄėHaven't you heard of them? Here is one: Why is a ball of yarn like the letter ‚Äėt?‚Äô Because a ball of yarn is circular, a circular is a sheet, a sheet is flat, a flat is $50 a month, $50 a month is dear, a deer is swift, a swift is a swallow, a swallow is a taste, a taste is an inclination, an inclination is an angle, an angle is a point, a point is an object aimed at, an object aimed at is a target, a target is a mark, a mark is an impression, an impression is a stamp, a stamp is a thing stuck on, a thing stuck on is a young man in love, and a young man in love is like the letter ‚Äėt‚Äô because he stands before ‚Äėu,‚Äô Miss Gracie.‚ÄĚ
‚ÄúI don't think you have the answer quite right,‚ÄĚ said the young lady. ‚ÄúA ball of yarn is round, a round is a steak, a stake is a wooden thing, a wooden thing is a young man in love, and a young man in love is like the letter ‚Äėt‚Äô because, Mr. Spoonamore‚ÄĚ‚Ä”and she spoke clearly‚Ä”‚Äúbecause he is often crossed.‚ÄĚ
The young man understood.
He took his hat and his progressive conundrums and vanished from Miss Gracie Garlinghouse's alphabet for ever.
3.

Here is a pretty mathematical problem which will interest the school children, as well as some of the teachers, for the reason that the popular answer is quite incorrect as the principle involved is not generally understood.
A bicycle rider went a mile in three minutes with the wind, and returned in four minutes against the wind How fast could he ride a mile if there was no wind?
Contrary to the popular answer to problems of this kind, that if a rider goes a mile in three minutes with the wind, and returns against the wind in four minutes, that 3 and 4 equal 7, should give a correct average, so that his time should be taken to be 3 1/2 minutes. We find this answer to be incorrect, because the wind has helped him for only three minutes, while it has worked adversely for four minutes. If he could ride a mile in three minutes with the wind, it is clear that he could go a mile and a third in four minutes, and one mile in four minutes against the wind. Therefore two and one-third miles in eight minutes gives his actual speed, because the wind helped him just as much as it has retarded him, so his actual speed for a single mile without any wind would be 3 minutes and 26 seconds.
[Page 199]