AS SHOWING HOW mathematics may be discussed in a digestible form, let us look into the following unique problem, which comes in with the new regime introduced by the recently formed Pie Trust:

It having come to the knowledge of the Boarders' Protective Union that the chef of Madame O'Flaharity's Pension Francais was cutting too many pieces out of one pie, which conflicts with Article V. Of the by-laws, which says: "A union pie must be divided with six straight cuts of a knife," the walking delegates of the association ordered a strike among the hoarders until the grievance was corrected.

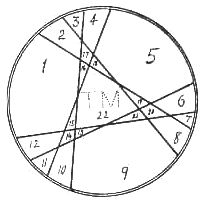
The sketch shows the madame explaining the limit of possibilities in dividing a No. 6 union pie, which problem will appeal directly to the hearts of the American pie-loving people irrespective of the beauty and importance of the proposition from a mathematical standpoint.

Madame O'Flaharity is discoursing upon the advantages of extending the greatest possible latitude to the practical application of the six-straight-cut-rule which affords an opportunity of varying the size and number of pieces according to circumstances. As a matter of fact, the opportunity for dispensing pieces of pie of variable size is generally utilized to advantage by clever landladies who have mastered the problem. The star boarders, and such as pay their bills promptly, get the big pieces with plenty of nice crust, while such as are badly in arrears get frozen nut, so far as pie is concerned. And what a volume of sentiment and appreciation can be expressed by the large thick piece which the hostess serves to the young doctor who is supposed to be attentive to her daughter Mary Jane!

But we are not dealing with the lessons and morals to be found between the crusts of a hoarding house pie, we are giving a kindergarten illustration of Euclid's rule, which says in mathematical lingo: ''Every line must intersect every other line, but no two intersections must coincide," which to the young folks not up in mathematical lore may be interpreted as meaning that "the old folks must be helped first and the children should not ask for second pieces.''

2. Royal Road

The following free translation of a German poem, which appeared during the last century in a Heidelberg college paper, shows the high estimation placed upon the study of puzzles in that eminent seat of learning:

Children must be busy.

     Always something learning;

Toys and playthings for their secrets.

     Inside-outward turning.

While the top is spinning

     The scholars wonder all,

How it stands erect unaided,

     Why it does not fall.

While the top is humming.

     Still the wonder grows.

By what art the little spinner

     Whistles as it goes.

Children learn while playing;

     Joining sport with learning;

Pastimes, often more than lessons,

     Into knowledge turning-

Puzzles, tricks and riddles.

     Make the children clever,

Leading by the Royal road, where

     Study is a pleasure.