



WE CALL ATTENTION to the following little little grindstone puzzle given just to show that the great bugaboo of squaring the circle can be explained and taught in a simple way, so as to be of inestimable service in the ordinary workshop.
It is told that two honest Syrians pooled their issues and bought a grindstone, but as they lived several miles apart, they agreed that, the elder man should keep the grindstone stone until he had reduced it in size just one-half, when it should be turned over to the other.
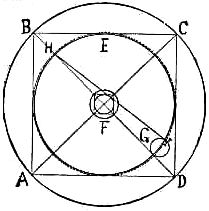
The grindstone was exactly 22 inches in diameter, with a 3 1-7 hole in the center for the shaft, as shown in the picture. What would be the size of the stone when given to the second owner
Our Syrian friends could get the approximate number of square inches contained in a circle of 22 inches diameter; from this they would deduct the number of inches contained in the 3 and 1/7 hole. Then they would figure out the approximate size of a circle containing half of the number of square inches, which would be the size of the grindstone when the first man is done with it. The only perfect method, however, is based upon our demonstration that the area of circles may be computed from the squares of their diameters. Knowing from our Pythagorean problem, that a square drawn within a circle would contain another circle just half the size of the larger circle, let us take the grindstone, and after drawing the lines A to C and B to D, build the square, A, B, C, D; then draw the circle, E, just within that square, and it contains exactly one half the area of the large circle.
Having stated, however, that loss from the centre hole must be divided between the two owners of the grindstone, we draw a square inside of the circular hole, and inside of that small square describe another small circle, which is just half the size of the circle, F. We will now work the Pythagoras rule for adding circles, and place the small circle at G, and the line from H to I will form the hypotenuse line of a right-angled triangle, which gives the diameter of a circle, combining the area of the circle E and the smallest circle, which is half of F. This enlarges the circle E, so that the dotted line shows a circle which contains exactly one-half of the grindstone, and will have a diameter of 15 5/7 inches.
2. Hoch Der Kaiser.
To familiarize our young folks with the geography of the world, they are presented with another lesson in hidden cities. They are asked to discover in the description of the picture the locality of a noted city, where I remember to have seen Prince Henry riding in state with the royal family, followed by a great multitude shouting “Hoch der Kaiser” which, as you all know, means “Hurrah for the Emperor!”

Hoch der Kaiser conceals the name Berlin.
3.
Which dress lasts a lady the longest? Her house dress, because she never wears it out.
Why should a disabled sailor go into business in a small Way? Because he cannot be a whole sailor.
Why is an old bachelor always in the right? Because he is never mis-taken.
When is a young lady not a young lady? When she's a sweet tart (sweet heart).
[Page 172]