



THERE IS A CERTAIN irresistible fascination about investigating the affairs of the moon which few can resist, so when the famous Moon Hoax was sprung upon the public during the early part of the last century it was shown that the people were prepared to believe almost anything. It was based upon the alleged powers of a marvelous telescope which, it was claimed, would enable us to see the smallest articles upon the moon’s surface. The public seized upon the reports with such credulity that the projectors of the hoax gave vivid descriptions and pictures of the inhabitants of the moon and their wonderful surroundings, so skillfully presented that despite of their extravagant claims were believed for a long time.
The surmises regarding the state of affairs on the moon has been a popular fad with theorists and writers from time immemorial.
Aristo, in his “Orlando Furioso.” sent Astolfo on his venturesome trip four centuries ago, and the wonderful stories of what he saw in the “Valley of Lost Things” among the hills of the moon deceived many. Cyrano de Bergerac's voyage to the moon is one of the most amusing contributions to modern literature, but Jules Verne's account of an aerial trip is the most thrilling of the many lunar legends. The quickest journey of record, however, is that of Edgar Allen Poe's hero. Hans Pfeel, of Rotterdam, who by means of a balloon completed the trip in nineteen hours. It was the detailed matter-of-fact account of this journey which so worked upon the brain of a leaned professor named Spearwood that he fitted out an expedition, and actually undertook to make the trip, firmly convinced that at a certain distance he would pass out of the influence of the earth's attraction and pass into that of the moon.
My sketch is drawn from a description published at the time of his ascent, but as the puzzle has nothing to do with the adventure after he had cut loose from his earthly connections, I will say that a pretty problem is found to be involved in the data as given, which does not possess the difficulty which mathematicians would ascribe to it according to accepted methods.
He had a ball of wire twenty-four inches in diameter, the wire being only one-hundredth of an inch thick. It looks like a difficult problem to tell the length of a ball of one-hundredth inch wire, twenty-four inches in diameter, but as a matter of fact it is so simple that it yields readily to common sense, and I should like to see how close our puzzlists can come to guessing the length of wire, without going very deeply into the subject, and shall take occasion in giving the answer to present a simple demonstration practically devoid of mathematics, which any clever child might understand.
In the Moon Problem wherein Professor Spearwood undertook to reach the moon through the aid of a captive balloon, it was to give a common sense way of telling how many miles of wire one one-hundredths of an inch thick could be made out of a sphere twenty-four inches in diameter.
Well, all that is necessary is for the student to know that a round box termed a cylinder contains exactly one-half more than a sphere which it would hold, as shown in the illustration presented herewith.
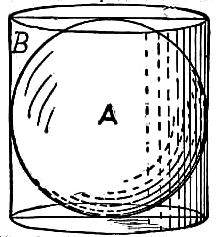
Therefore, if the sphere A is twenty-four inches in diameter, it occupies two thirds of the interior of that hat box B, which is twenty-four inches high. Therefore, the ball would be equal to a cylinder two-thirds that height, viz, twenty-four inches in diameter, but only sixteen inches high. That converts the ball into a cylinder, and as wire is really nothing but an extended cylinder, we readily find out the relative proportion between twenty-four inches and the one one-hundredth of an inch, as the one is 2,400 times larger in diameter than the other, so 2,400x2,400 gives 5,760,000 as the number of little cylinders one one-hundredth of an inch thick, contained in the big cylinder, and as they would be sixteen inches long, we multiply by sixteen and find that there would be 92,160,000 inches which will reduce readily to 1,454 miles 2,880 feet as the length of the wire.
The relative proportions of a sphere to a cylinder was discovered by Archimedes 380 years B. C., and was engraved upon his tomb to perpetuate to succeeding ages what the great mathematician looked upon as his most important discovery.
2. Just a Plain Sell
“How do you pronounce T O?”
“Too.”
“And T O O?”
“Too.”
“And T W O?”
“Too, of course.”
“Well, how do you pronounce the second day of the week?”
“Tuesday.”
“Really, now, I always thought the second day was Monday.”
[Page 145]