1.

Aesop, who lived some twenty-five hundred years ago, was a slave belonging to a noble Athenian, who, being struck by his originality and marvelous gift of inculcating morals or cutting satire in his stories of birds, animals and fishes, brought him to the notice of Croesus, King of Lydia. Among his oldest fables is the story of the ambitious eagle, which resolved to fly to the sun. Every morning as the sun rose in the east the eagle would fly towards it, going a thousand miles before the hour of noon, when the sun would be on the meridian, thus as the sun would pass on towards the west the eagle would continue its hopeless chase, and just as the sun would disappear below the western horizon the eagle would find itself back to the original starting point.

The story is all right as told, but his mathematics are slightly out of gear, and present a pretty problem for our puzzlists to study over. In the early start towards the sun, they are both advancing towards the meeting point, and we will accept the intimation that the sun goes five times faster than the eagle, so they will speedily be on the meridian, but a stern chase is a long chase, so the afternoon race will be the longer one, and will carry the eagle 500 miles farther west every day, so that it will be many a long day before Aesop’s point is actually accomplished and the foolish eagle returns to the starling point after making a complete circuit of the globe.

The circumference of the earth being known, and it being assumed that the eagle flies at a height from the earth’s surface which does not materially affect the distance, it is shown that the eagle would go 500 miles further west each day. Let us start the bird on his tour from the dome of the Capitol at Washington, Wednesday January 1st. 1896, on which day of the week would he return to the starting point?

Here is the way a Dutchman gave the problem: “Suppose two geese start from opposite windows of that dome at Washington, what direction would they have to fly to meet again in the shortest possible time?”

Third proposition: Do you know why it is that if you saw an island exactly one hundred miles away due north-east, you would never get there by sailing due north-east?

2.

The Puzzleland Sunday School Teacher is giving the children some good resolutions with which to begin the new year. It is a good idea to inject a little difficulty into the lesson so as to impress it well on the memory. Of course, it is any easy puzzle for the little folks, nevertheless let us see if you are clever enough to read it right off.

3. How to Make Diamonds

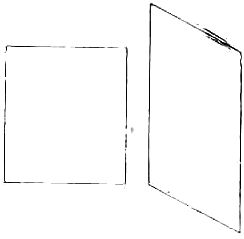
The juvenile readers will find in the following an interesting method of passing an hour or two out of school hours or to amuse an evening party. All that is needed is a pair of scissors and some paper which may be cut into the form of a parallelogram or rectangle as shown in the above illustrations.

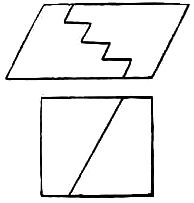
The puzzle is to discover how either one of the forms Can be divided into equal halves which will fit together so as to form a perfect diamond. As both diamonds will be of equal dimensions, it shows that the above forms are of the same size. It would have been a more difficult puzzle to have required you to prove the forms to be of the same size by merely cutting them into halves, It will be found that they are built upon different ideas, although based on Scientific principles of geometry well worth knowing.

Of course, it is understood that no paper is wasted, as the diamond, when completed, will be just as large as the present figure.

Cutting puzzles of this kind are always popular and instructive in that they exercise the inventive faculties and serve as an elementary drawing school

4. A Rebus

As to what lies beneath or concealed,

     Will oft prove as false as the base flatterer’s soul.

When facts, stubborn facts are revealed.

Cipher Answer. �”19, 21, 18, 6, 1, 3, 5.