



IN ACKNOWLEDGEMENT of a flattering criticism from Professor Rogers, which is going the rounds of the press, wherein he says. "Sam Loyd is doing more to encourage higher mathematics than all of our colleges put together,” accompanied by a hearty endorsement from a noted professor, I take occasion to discourse upon what he terms my life-long “hobby.”
Half a century’s interest in puzzle matters has shown me that in puzzles we have the only elementary school for the development of ingenuity and a love of the mathematical and mechanical arts. I have witnessed such a wonderful record of civil service examinations, as well as growth of master minds from the ranks of puzzledom, that, when I hear of a puzzlist trying for some competitive position, it seems like a foregone conclusion that his success is assured. On the other hand, my connection with mechanical matters frequently shows a class of graduates whose course of study appears to have made them so stupid as to be unfitted for their profession.
The “kindergarten school” of teaching aims to fascinate pupils with their studies, and is built upon the fundamental law that the mind should not be burdened with rules which are to be committed to memory. If the theory of the lesson is made clear, the student formulates his own rules and methods, just as one describes an incident in his own language.
The science of mathematics is heavily freighted with musty rules, so ponderous and obscure that few even with explanations, grasp their meaning, and are glad to dismiss them from their minds when they leave school or college. When a principle is thoroughly understood difficulty ceases to exist, for even in what are termed abstruse calculations we can do nothing but add or multiply, so, while it may take more time to multiply 888,888 by 777,777 it, is really as easy as to multiply 8 by 7. The difficulty of a complex sum is due entirely to lack of knowledge, or familiarity with the principle involved.
Mechanical science and the principles of higher mathematics may be taught through the medium of a simple puzzle, and to relieve the dry technicalities a little fun may be injected into the puzzle story which will do much toward cultivating an appreciation of humor. The problem should be clothed in suitable dress to make the result sought, appear probable and more readily understood. It is well also to base the proposition upon some mechanical truth, historical incident or bit of classical lore such as may improve the general knowledge of the student, for in this way a thousand and one little tid-bits of information may be picked up and unconsciously stored away in the mind in a way never to be forgotten.
Twenty-four hundred years ago Pythagoras discovered that if he drew squares upon the three sides of a right-angled triangle the larger square will be exactly equal in area to the two smaller squares combined.
He was so elated over the proof of the larger square being equal to the other two, no matter what might be the dimensions of the triangle that he gave away all of his worldly goods and chattels in offerings to the gods, and yet he was ridiculed and told to show his discovery to the dogs.
Pythagoras Classical two-square problem solves itself by the application of the rule which shows that the combined squares of the smaller sides of a right-angled triangle are equal to the square of the largest. Taking our scissors we cut from A to B, which produces a triangle whose base and elevation are equal to the sides of the two squares as given in the puzzle. The line of the hypotenuse, therefore, should show the dimensions of the large square which combines the other two squares. We therefore cut from B to C and clip off another triangle and fit the three pieces together so as to form the large square A B C D.
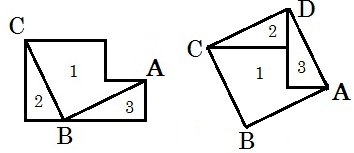
This rule holds good to give the combined size of any two squares.
[Page 101]