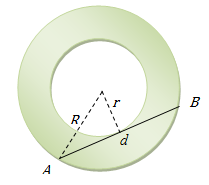
Figure 2

In Figure 2, R is the radius of the outer circle, r is the radius of the inner circle (line segment is drawn perpendicular from the center to AB), and d is the length of AB. We can immediately write

\[ \left(\frac{d}{2}\right)^2+r^2=R^2, \] \[ d=2\sqrt{R^2-r}. \]

For the shaded area, we then write

\[ A = \pi R^2-\pi r^2 \] \[ \frac{A}{\pi} = R^2-r^2 \]

Substituting the last equation into the second equation gives $d=2\sqrt{A/\pi} \Rightarrow A=d^2/4\pi$, but this is just the standard formula for the area of a circle with diameter $d$.